1.3 The Stern-Gerlach experiment

The usual reason for considering the Stern-Gerlach experiment is that it shows experimentally that angular momentum is quantised, and that particles can have intrinsic angular momentum which is an integer multiple of $\frac{1}{2}\hslash$. An inhomogeneous magnetic field deflects particles by an amount proportional to the component of their magnetic moment parallel to the field; when a beam of atoms passes through they follow only a few discrete paths ($2j+1$ where $j$ is their total angular momentum quantum number) rather than, as classically predicted, a continuum of paths (corresponding to a magnetic moment which can be at any angle relative to the field).

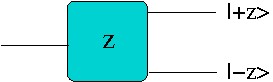
For our purposes though a Stern-Gerlach device is a quick and easily-visualised way of making measurements of quantities (spin components) for which the corresponding operators do not commute, and thereby testing the postulates concerned with measurement. We restrict ourselves to spin-$\frac{1}{2}$; all we need to know is that if we write $\left|\right.+n⟩$ to indicate a particle with its spin up along the direction $n$, and $\left|\right.-n⟩$ for spin down, then the two orthogonal states $\left\{\left|\right.\pm n⟩\right\}$ span the space for any $n$, and ${\left|⟨\pm n|\pm n^{\prime }⟩\right|}^2=\frac{1}{2}$ if $n$ and $n^{\prime }$ are perpendicular.

In the figure above we see an unpolarised beam entering a Stern-Gerlach device with its field oriented in the $z$-direction. If we intercept only the upper or lower exiting beam, we have a pure spin-up or spin-down state.

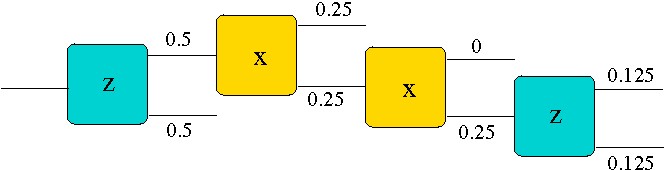
Here we see a sequence of Stern-Gerlach devices with their fields oriented in either the $x$- or $z$-direction. The numbers give the fraction of the original unpolarised beam which reaches this point. The sequence of two $x$-devices in a row illustrates reproducibility. The final $z$-device is the really crucial one. Do you understand why half of the particles end up spin-down, even though we initially picked the $\left|\right.+z⟩$ beam?

• Townsend ch 1.4

[next] [prev] [up] [top]