The Einstein-Poldosky-Rosen “paradox” and Bell’s inequalities

6.1 The Einstein-Poldosky-Rosen “paradox” and Bell’s inequalities

Summary: This section is about nothing less important than “the nature of reality”!

In 1935 Einstein, along with Boris Poldosky and Nathan Rosen, published a paper entitled “Can quantum-mechanical description of physical reality be considered complete?” By this stage Einstein had accepted that the uncertainty principle did place fundamental restrictions on what one could discover about a particle through measurements conducted on it. The question however was whether the measuring process actually somehow brought the properties into being, or whether they existed all along but without our being able to determine what they were. If the latter was the case there would be “hidden variables” (hidden from the experimenter) and the quantum description—the wave function—would not be a complete description of reality. Till the EPR paper came out many people dismissed the question as undecidable, but the EPR paper put it into much sharper focus. Then in 1964 John Bell presented an analysis of a variant of the EPR paper which showed that the question actually was decidable. Many experiments have been done subsequently, and they have come down ﬁrmly in favour of a positive answer to the question posed in EPR’s title.

The original EPR paper used position and momentum as the two properties which couldn’t be simultaneously known (but might still have hidden deﬁnite values), but subsequent discussions have used components of spin instead, and we will do the same. But I will be quite lax about continuing to refer to “the EPR experiment”.

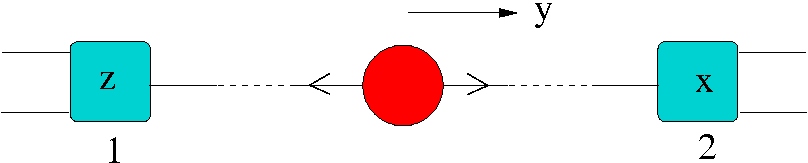
There is nothing counter-intuitive or unclassical about the fact that we can produce a pair of particles whose total spin is zero, so that if we ﬁnd one to be spin-up along some axis, the other must be spin down. All the variants of the experiment to which we will refer can be considered like this: such a pair of electrons is created travelling back-to-back at one point, and travel to distant measuring stations where each passes through a Stern-Gerlach apparatus (an “SG”) of a certain orientation in the plane perpendicular to the electrons’ momentum.

As I say there is nothing odd about the fact that when the two SGs have the same orientation the two sequences recorded at the two stations are perfectly anti-correlated (up to measurement errors). But consider the case where they are orientated at 90 $^{\circ}$ with respect to each other as below:

Suppose for a particular pair of electrons, we measure number 1 to be spin up in the $z$ -direction and number 2 to be spin down in the $x$ -direction. Now let’s think about what would have happened if we had instead measured the spin in the $x$ -direction of particle 1. Surely, say EPR, we know the answer. Since particle 2 is spin down in the $x$ -direction, particle 1 would have been spin up. So now we know that before it reached the detector, particle 1 was spin up in the z-direction (because that’s what we got when we measured it) and also spin up in the x-direction (because it is anti-correlated with particle 2 which was spin down). We have beaten the uncertainty principle, if only retrospectively.

But of course we know we can’t construct a wave function with these properties. So is there more to reality than the wave function? Bell’s contribution was to show that the assumption that the electron really has deﬁnite values for diﬀerent spin components—if you like, it has an instruction set which tells it which way to go through any conceivable SG that it might encounter—leads to testable predictions.

For Bell’s purposes, we imagine that the two measuring stations have agreed that they will set their SG to one of 3 possible settings. Setting $A$ is along the $z$ -direction, setting $C$ is along the $x$ direction, and setting $B$ is at 45 $^{\circ}$ to both. In the ideal set-up, the setting is chosen just before the electron arrives, suﬃciently late that no possible causal inﬂuence (travelling at not more than the speed of light) can reach the other lab before the measurements are made. The labs record their results for a stream of electrons, and then get together to classify each pair as, for instance, $(A ↑, B ↓)$ or $(A ↑, C ↑)$ or $(B ↑, B ↓)$ (the state of electron 1 being given ﬁrst). Then they look at the number of pairs with three particular classiﬁcations: $(A ↑, B ↑)$ , $(B ↑, C ↑)$ and $(A ↑, C ↑)$ . Bell’s inequality says that, if the way the electrons will go through any given orientation is set in advance,

N (A ↑, B ↑) + N (B ↑, C ↑) \geq N (A ↑, C ↑)

where $N (A ↑, B ↑)$ is the number of $(A ↑, B ↑)$ pairs etc.

Now let’s prove that.

Imagine any set of objects (or people!) with three distinct binary properties $a$ , $b$ and $c$ —say blue or brown eyes, right or left handed, and male or female (ignoring messy reality in which there are some people not so easily classiﬁed). In each case, let us denote the two possible values as $A$ and $\bar{A}$ etc ( $\bar{A}$ being “not $A$ ” in the sense it is used in logic). Then every object is classiﬁed by its values for the three properties as, for instance, $A B C$ or $A \bar{B} \bar{C}$ or $\bar{A} B C \dots$ . The various possibilities are shown on a Venn diagram below (sorry that the bars are through rather than over the letters...)

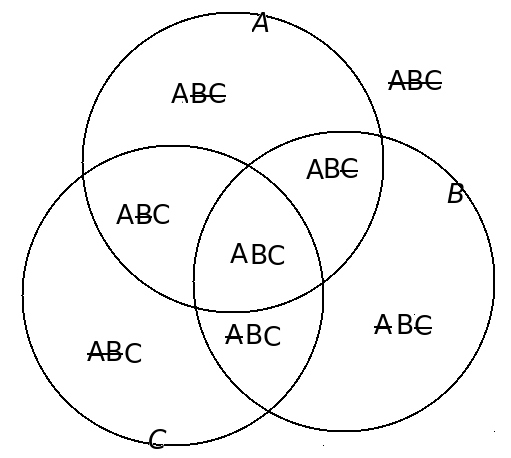
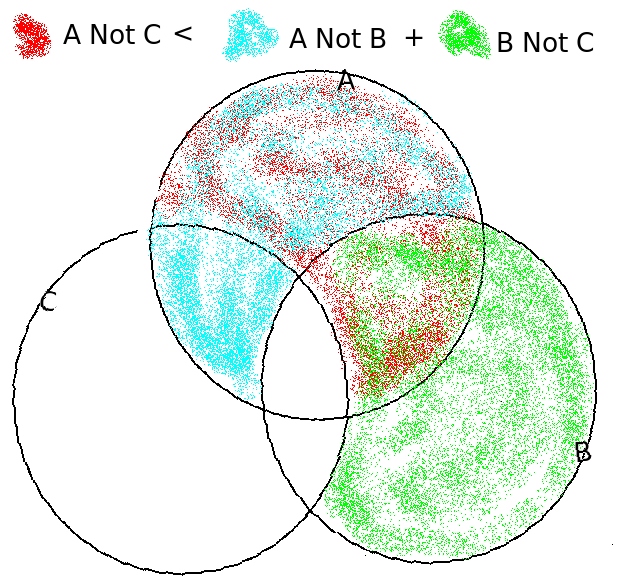
In any given collection of objects, there will be no fewer than zero objects in each subset, obviously. All the $N$ s are greater than or equal to zero. Now we want to prove that the number of objects which are $A \bar{B}$ (irrespective of $c$ ) plus those that are $B \bar{C}$ (irrespective of $a$ ) is greater than or equal to the number which are $A \bar{C}$ (irrespective of $b$ ):

N (A \bar{B}) + N (B \bar{C}) \geq N (A \bar{C})

This is obvious from the diagram below, in which the union of the blue and green sets fully contains the red set.

A logical proof is as follows:

\begin{array}{rcl} N (A \bar{B}) + N (B \bar{C}) & = & N (A \bar{B} C) + N (A \bar{B} \bar{C}) + N (A B \bar{C}) + N (\bar{A} B \bar{C}) \\ = & N (A \bar{B} C) + N (A \bar{C}) + N (\bar{A} B \bar{C}) \geq N (A \bar{C}) \end{array}

To apply to the spins we started with, we identify $A$ with $A ↑$ and $\bar{A}$ with $A ↓$ . Now if an electron is $A ↑ B ↓$ (whatever $C$ might be) then its partner must be $A ↓ B ↑$ , and so the result of a measurement $A$ on the ﬁrst and $B$ on the second will be $(A ↑, B ↑)$ . Hence the inequality for the spin case is a special case of the general one. We have proved Bell’s inequality assuming, remember, that the electrons really do have these three deﬁned properties even if, for a single electron, we can only measure one of them.

Now let’s consider what quantum mechanics would say. We ﬁrst remind ourselves of the relation between the spin-up and spin-down states for two directions:

\begin{array}{l} | θ, ↑ ⟩ = cos \frac{θ}{2} | 0, ↑ ⟩ + sin \frac{θ}{2} | 0, ↓ ⟩ & | 0, ↑ ⟩ = cos \frac{θ}{2} | θ, ↑ ⟩ - sin \frac{θ}{2} | θ, ↓ ⟩ \\ | θ, ↓ ⟩ = - sin \frac{θ}{2} | 0, ↑ ⟩ + cos \frac{θ}{2} | 0, ↓ ⟩ & | 0, ↓ ⟩ = sin \frac{θ}{2} | θ, ↑ ⟩ + cos \frac{θ}{2} | θ, ↓ ⟩ \end{array}

where $θ$ is the angle between the orientation of the two axes. For $A$ and $B$ or for $B$ and $C$ $θ = 4 5^{\circ}$ ; for $A$ and $C$ it is $9 0^{\circ}$ .

Consider randomly oriented spin-zero pairs and settings $A$ , $B$ and $C$ equally likely. If the ﬁrst SG is set to A and the second to B (which happens 1 time in 9), there is a probability of $1 ∕ 2$ of getting $A ↑$ at the ﬁrst station. But then we know that the state of the second electron is $| A ↓ ⟩$ and the probability that we will measure spin in the $B$ direction to be up is ${sin}^{2} 22 . 5^{\circ}$ . Thus the fraction of pairs which are $(A ↑, B ↑)$ is $\frac{1}{2} {sin}^{2} 22 . 5^{\circ} = 0.073$ , and similarly for $(B ↑, C ↑)$ . But the fraction which are $(A ↑, C ↑)$ is $\frac{1}{2} {sin}^{2} 4 5^{\circ} = 0.25$ . So the prediction of quantum mechanics for $9 N_{0}$ measurements is

N (A \bar{B}) + N (B \bar{C}) = 0.146 N_{0} < N (A \bar{C}) = 0.25 N_{0}

So Bell’s inequality does not hold. The experiment has been done many times, starting with the pioneering work of Alain Aspect, and every time the predictions of quantum mechanics are upheld and Bell’s inequality is violated. (Photons rather than electrons are used. Early experiments fell short of the ideal in many ways, but as loopholes have been successively closed the result has become more and more robust.)

It seems pretty inescapable that the electrons have not “decided in advance” how they will pass through any given SG. Do we therefore have to conclude that the measurement made at station 1 is responsible for collapsing the wave function at station 2, even if there is no time for light to pass between the two? It is worth noting that no-one has shown any way to use this set-up to send signals between the stations; on their own they both see a totally random succession of results. It is only in the statistical correlation that the weirdness shows up...

In writing this section I found this document by David Harrison of the University of Toronto very useful.

(Gasiorowicz ch 20.3,4)
Mandl ch 6.3
Townsend ch 5.4,5

Further discussions can be found in N. David Mermin’s book Boojums all the way through (CUP 1990) and in John S. Bell’s Speakable and unspeakable in quantum mechanics (CUP 1987).

[up] [top]