Preliminaries

Summary: Scattering experiments provide us with almost all the information we have about the nature of sub-atomic matter. Here we will only consider elastic scattering.

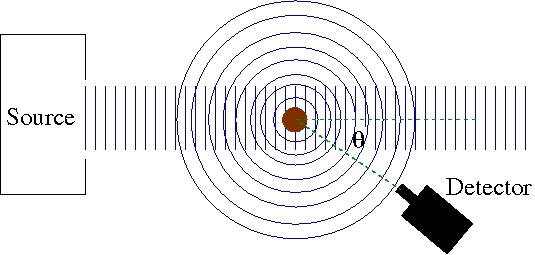
All we know about the structure of sub-atomic matter comes from scattering experiments, starting with Rutherford’s discovery of the nucleus right up to the Tevatron and LHC. In this course we will introduce the main ideas, but largely conﬁne ourselves to elastic scattering of particles from a ﬁxed, localised potential

V (r)

; this is the limit of two-body scattering where one particle (the projectile) is much lighter than the other (the stationary target). We will be looking for the probability that the particle is scattered away from its original direction.

A careful approach would involve a wavepacket for the projectile, and the problem would involve a fully time-dependent approach as the wavepacket aproached the scattering centre, interacted with it and then moved away out of its inﬂuence. An easier approach is to use an incident plane wave to represent a coherent beam of particles of ﬁxed momentum; the wavepacket aproach must give the same results in the limit that the momentum spread in the packet is small. The lateral spread of the wavefronts will be large compared to the range of

V (r)

but small compared to the perpendicular distance from the beam to the detector, so that unless we put the detector directly in the line of the beam, we will only detect scattered particles.

We deﬁne the scattering cross section as the rate of particles scattered from the ﬁeld divided by the incoming ﬂux. Since the units of ﬂux are particles per second per metre

^{2}

, the cross section has units of area. This has an obvious geometric interpretation. (The non-SI units of cross-section used in particle physics are barns, where 1 barn is

1 0^{- 28}

^{2}

- that’s as in “barn door”, something you can’t miss!) We are often interested in angular distributions too – they are rarely isotropic as depicted above – so then we are interested in the scattering rate into a given solid angle. Conventionally

θ

measures the angle from the beam direction, as shown above, and

ϕ

the angle in a plane perpendicular to the beam direction.

An inﬁnitesimal solid angle, spanned by inﬁnitesimal range of

θ

and

ϕ

, is

d Ω = sin θ d θ d ϕ

. If we have a detector at distance

r

with a (small) opening of area

d S

facing the scattering source it subtends a solid angle

d Ω = d S ∕ r^{2}

. If the scattering rate into this detector divided by the initial ﬂux is denoted

d σ

, the diﬀerential cross section is

d σ ∕ d Ω

. Obviously

\int (d σ ∕ d Ω) d Ω = σ

if the integral is taken over all angles.

Outside the range of

V (r)

the scattered particles are free and have the same energy as initially (elastic scattering). The wavefunction must satisy Schrödinger’s equation which can be written

(\nabla^{2} + k^{2}) ψ_{s c} = 0

(with

ℏ^{2} k^{2} ∕ 2 m = E

). Now we know that

e^{i k \cdot r}

is a plane wave solution of this, but we are looking for outgoing waves emanating from the centre. These are spherical harmonics times spherical Bessel functions, and have the asymptotic form (as

r \to \infty

)

ψ_{s c} \to \sum_{l m} A_{l m} (k) Y_{l}^{m} (θ, ϕ) \frac{e^{i k r}}{r} = f (k, θ, ϕ) \frac{e^{i k r}}{r}

The function

f (k, θ, ϕ)

is called the scattering amplitude - note it has dimensions of length. (The fact that as

r \to \infty

the radial wavefunction doesn’t depend on

l

can be seen from the fact that

\nabla^{2} \to d^{2} ∕ d r^{2}

; the angular part falls oﬀ as

1 ∕ r^{2}

\frac{ℏ}{2 i m} (ψ_{s c}^{*} \nabla ψ_{s c} - ψ_{s c} \nabla ψ_{s c}^{*}) \overset{r \to \infty}{\to} {|f (k, θ, ϕ)|}^{2} \frac{ℏ k}{m r^{2}} \hat{r}

which is indeed outgoing (had we chosen

e^{- i k r}

it would have been ingoing). If we have a detector with a (small) opening of area

r^{2} d Ω

facing the scattering source the rate of particles hitting it is

{|f (θ, ϕ)|}^{2} (ℏ k ∕ m) d Ω

. Since the ﬂux in the beam wave

e^{i k \cdot r}

\frac{ℏ k}{m}

, we have

d σ = {|f (k, θ, ϕ)|}^{2} d Ω and \frac{d σ}{d Ω} = {|f (k, θ, ϕ)|}^{2}

So the scattering amplitude squared is the diﬀerential cross section. Now all we have to do is calculate it!

5.1 Preliminaries