Heisenberg vs Schrodinger pictures

4.7 Heisenberg vs Schrödinger pictures

When at the start we, for convenience, absorbed the time dependence due to ${\hat{H}}^{(0)}$ into the deﬁnition of the coeﬃcients (switching from $c_{n} (t)$ to $d_{n} (t) = e^{i E_{n}^{(0)} t ∕ ℏ} c_{n} (t)$ ), we did something which has a rather fancy name: we switched to the interaction picture.

The Schrödinger picture is the one we are used to. Our basis kets $| n ⟩$ (eigenkets of the Hamiltonian $\hat{H}$ ) are time-independent but quantum states are built from them with time-dependent coeﬃcients: $| ψ_{S} (t) ⟩ = \sum_{n} c_{n} (t) | n ⟩$ . These satisfy the Schrödinger equation $i ℏ \frac{d}{d t} | ψ_{S} (t) ⟩ = \hat{H} | ψ_{S} (t) ⟩$ which implies $| ψ_{S} (t) ⟩ = U (t, t_{0}) | ψ_{S} (t_{0}) ⟩$ where $U (t, t_{0}) = T exp {- (i ∕ ℏ) \int_{t_{0}}^{t} \hat{H} (t^{'}) d t^{'}}$ . In this picture the Hamiltonian itself is not usually time-dependent (in the absence of external forcing) nor are the other operators such as $\hat{x}$ , $\hat{p}$ . The expectation value of operators can change though of course - as we’ve seen $d ⟨ \hat{Ω} ⟩ ∕ d t = ⟨ [\hat{Ω}, \hat{H}] ⟩$

One can also however work in an alternative picture, the Heisenberg picture, in which the quantum states are time-independent: $| ψ_{H} ⟩ = U^{†} (t, t_{0}) | ψ_{S} (t) ⟩ = | ψ_{S} (t_{0}) ⟩$ . The rational for this is that nothing really changes fundamentally in such a state, in particular the chance of obtaining energy $E_{n}$ is constant. Clearly this state does not obey the TDSE or any equation giving evolution in time. However the results for the time-dependence of observables must be the same as before, so in the Heisenberg picture operators all carry time-dependence: $Ω_{H} (t) = U^{†} (t, t_{0}) Ω_{S} U (t, t_{0})$ . Thus it is the time-dependence of the operator itself that is given by the commutator with $\hat{H}$ , ie $\frac{d}{d t} {\hat{Ω}}_{H} = [{\hat{Ω}}_{H}, \hat{H}]$ . (Note $\hat{H}$ itself is clearly the same in both pictures, and only time-dependent if there are external forcing terms.)

The interaction picture is somewhere in between. As we have done throughout this section, we split the Hamiltonian into two parts, typically the “free” Hamiltonian ${\hat{H}}^{(0)}$ which will be time-independent, and a (possibly time-dependent) “interaction” Hamiltonian ${\hat{H}}^{(1)}$ . We then work in a picture which would be Heisenberg’s if ${\hat{H}}^{(1)}$ vanished, but use the Schrödinger picture to include the eﬀects of ${\hat{H}}^{(1)}$ . Thus

| ψ_{I} (t) ⟩ = {U^{(0)}}^{†} (t, t_{0}) | ψ_{S} (t) ⟩ = \sum_{n} d_{n} (t) | n ⟩ and Ω_{I} (t) = {U^{(0)}}^{†} (t, t_{0}) Ω_{S} U^{(0)} (t, t_{0})

with

i ℏ \frac{d}{d t} | ψ_{I} (t) ⟩ = {\hat{H}}_{I}^{(1)} | ψ_{I} (t) ⟩ and \frac{d}{d t} {\hat{Ω}}_{I} = [{\hat{Ω}}_{I}, {\hat{H}}_{I}^{(0)}]

Note that now we do have to specify ${\hat{H}}_{I}^{(1)} (t) = {U^{(0)}}^{†} (t, t_{0}) H_{S}^{(1)} (t_{0}) U^{(0)} (t, t_{0})$ because in general $[{\hat{H}}^{(0)}, {\hat{H}}_{S}^{(1)}] \neq 0$ .

Concentrating on the time evolution of the state, we deﬁne $U_{I} (t, t_{0})$ such that $| ψ_{I} (t) ⟩ = U_{I} (t, t_{0}) | ψ_{I} (t_{0}) ⟩$ . It is clear that this satisﬁes

i ℏ \frac{d}{d t} U_{I} (t, t_{0}) = {\hat{H}}_{I}^{(1)} (t) U_{I} (t, t_{0})

which is formally solved by

U_{I} (t, t_{0}) = 1 - \frac{i}{ℏ} \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) U_{I} (t^{'}, t_{0}) d t^{'}

(just diﬀerentiate both sides by $t$ ; the $1$ comes from the initial condition that $U_{I} (t_{0}, t_{0}) = 1$ .)

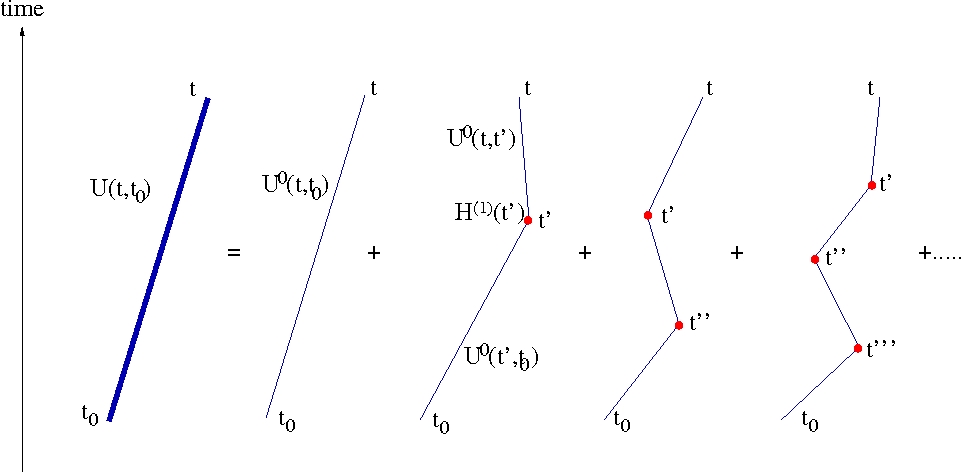
The utility of this comes if $H_{I}^{(1)} (t^{'})$ is small, since we can then develop a perturbative sequence for $U_{I}$ , the zeroth approximation being just $1$ , the ﬁrst correction coming from substituting $1$ for $U_{I}$ in the integral, the second approximation from substituting the ﬁrst approximation for $U_{I}$ in the integral and so on:

\begin{array}{rcl} U_{I} (t, t_{0}) & = & 1 - \frac{i}{ℏ} \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) d t^{'} - \frac{1}{ℏ^{2}} \int_{t_{0}}^{t} \int_{t_{0}}^{t^{'}} {\hat{H}}_{I}^{(1)} (t^{'}) {\hat{H}}_{I}^{(1)} (t^{″}) d t^{'} d t^{″} \\ + \frac{i}{ℏ^{3}} \int_{t_{0}}^{t} \int_{t_{0}}^{t^{'}} \int_{t_{0}}^{t^{″}} {\hat{H}}_{I}^{(1)} (t^{'}) {\hat{H}}_{I}^{(1)} (t^{″}) {\hat{H}}_{I}^{(1)} (t^{‴}) d t^{'} d t^{″} d t^{‴} + \dots \end{array}

Reverting to the Schrödinger picture, this reads

\begin{array}{rcl} U (t, t_{0}) & = & U^{(0)} (t, t_{0}) U_{I} (t, t_{0}) \\ = & U^{(0)} (t, t_{0}) - \frac{i}{ℏ} \int_{t_{0}}^{t} U^{(0)} (t, t^{'}) {\hat{H}}_{S}^{(1)} (t^{'}) U^{(0)} (t^{'}, t_{0}) d t^{'} \\ - \frac{1}{ℏ^{2}} \int_{t_{0}}^{t} \int_{t_{0}}^{t^{'}} U^{(0)} (t, t^{'}) {\hat{H}}_{S}^{(1)} (t^{'}) U^{(0)} (t^{'}, t^{″}) {\hat{H}}_{S}^{(1)} (t^{″}) U^{(0)} (t^{″}, t_{0}) d t^{'} d t^{″} \\ + \frac{i}{ℏ^{3}} \int_{t_{0}}^{t} \int_{t_{0}}^{t^{'}} \int_{t_{0}}^{t^{″}} U^{(0)} (t, t^{'}) {\hat{H}}_{S}^{(1)} (t^{'}) U^{(0)} (t^{'}, t^{″}) {\hat{H}}_{S}^{(1)} (t^{″}) U^{(0)} (t^{″}, t^{‴}) {\hat{H}}_{S}^{(1)} (t^{‴}) U^{(0)} (t^{‴}, t_{0}) d t^{'} d t^{″} d t^{‴} + \dots \end{array}

where we have used the combination property of the unitary time-evolution operators, $U^{(0)} (t, t_{0}) {U^{(0)}}^{†} (t^{'}, t_{0}) = U^{(0)} (t, t^{'})$ if $t^{'}$ is between $t$ and $t_{0}$ . We see that we have a picture where the free Hamiltonian ${\hat{H}}^{(0)}$ governs the time evolution for most of the time, interrupted by interactions ( ${\hat{H}}^{(1)}$ ) on occasions, with multiple interactions being less progressively less likely. This is illustrated below.

Note that eigenstates of $H_{S}^{(0)}$ remain so under the action of $U^{(0)} (t^{'}, t^{″})$ : $U^{(0)} (t^{'}, t^{″}) | n^{(0)} ⟩ = e^{- i (t^{'} - t^{″}) E_{n}^{(0)} ∕ ℏ} | n^{(0)} ⟩$ . So if the system starts oﬀ in a particular state $| i^{(0)} ⟩$ it will remain in it till it reaches the ﬁrst interaction. At that point it can undergo a transition into any other state $| n^{(0)} ⟩$ for which $⟨ n^{(0)} | H^{(1)} | i^{(0)} ⟩ \neq 0$ . If we are looking for the probability that the system ends up in state $| f^{(0)} ⟩$ then in the ﬁrst term in the expansion we need $i = f$ , in the second we need them to be linked by $⟨ f^{(0)} | H^{(1)} | i^{(0)} ⟩$ , but in the third and subsequent terms the transition from $| i^{(0)} ⟩$ to $| f^{(0)} ⟩$ can be via one or more intermediate states. Energy does not have to be conserved in these intermediate steps, only in the overall transition: the system can “borrow” energy from the ﬁeld for a short time, as reﬂected in the expression $Δ E Δ t \sim ℏ$ . Exactly the same idea is behind the picture of elementary particles interacting via virtual particles, as depicted in Feynman diagrams.

This is a good opportunity to introduce the time-ordered exponential. If we introduce the time-ordering operator, such that $T Â (t) \hat{B} (t^{'}) = Â (t) \hat{B} (t^{'})$ if $t^{'} < t$ and $\hat{B} (t^{'}) Â (t)$ if $t^{'} > t$ (and assuming they commute if $t^{'} = t$ ), then we can write

\int_{t_{0}}^{t} \int_{t_{0}}^{t^{'}} \hat{H} (t^{'}) \hat{H} (t^{″}) d t^{'} d t^{″} = \frac{1}{2} T \int_{t_{0}}^{t} \int_{t_{0}}^{t} \hat{H} (t^{'}) \hat{H} (t^{″}) d t^{'} d t^{″};

extending the $t^{″}$ integral from $t^{'}$ to $t$ generates terms in which the two Hamiltonians are in the wrong order but the $T$ operator switches them so the net eﬀect is that we over-count by a factor of two. Similarly with three factors we can extend the integrals to $t$ but over count by $3!$ , and so on. Hence we can write

\begin{array}{rcl} U_{I} (t, t_{0}) & = & 1 - \frac{i}{ℏ} T \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) d t^{'} - \frac{1}{2!} \frac{1}{ℏ^{2}} T \int_{t_{0}}^{t} \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) {\hat{H}}_{I}^{(1)} (t^{″}) d t^{'} d t^{″} \\ + \frac{1}{3!} \frac{i}{ℏ^{3}} T \int_{t_{0}}^{t} \int_{t_{0}}^{t} \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) {\hat{H}}_{I}^{(1)} (t^{″}) {\hat{H}}_{I}^{(1)} (t^{‴}) d t^{'} d t^{″} d t^{‴} + \dots \\ = & T exp (\frac{i}{ℏ} \int_{t_{0}}^{t} {\hat{H}}_{I}^{(1)} (t^{'}) d t^{'}) . \end{array}

Identical algebra is used in writing the full evolution operator as $U (t, t_{0}) = T exp (\frac{i}{ℏ} \int_{t_{0}}^{t} \hat{H} (t^{'}) d t^{'})$ as was asserted in section 1.2.

(Gasiorowicz ch 16.3)
Shankar ch 18.3
Townsend ch 14.5

[prev] [up] [top]