4.6 Selection rules

The heart of all our expressions for interaction with the electromagnetic field was the matrix element $eℰ⟨f|\epsilon \cdot r|i⟩$, obtained from a spatially invariant electric field which we argued was the long-wavelength limit of an electromagnetic wave. Since the wavelength of light generated from atomic transitions if of the order of $10^{-7}-10^{-8}$ m, while atomic sizes are of order $10^{-10}$ m, this should be a good approximation.

For completeness we note that the expression $E=-\nabla \varphi \left(r\right)$ is no longer actually valid for time-dependent fields; the correct expression is $E=-\nabla \varphi \left(r\right)-\text{d}A∕\text{d}t$ where $A$ is the vector potential; furthermore a very convenient gauge for radiation is $\varphi =0,A=A_0\epsilon {\text{e}}^{i\left(k\cdot r-\omega t\right)}$ with $k\cdot \epsilon =0$ and $A_0=ℰ∕\omega$. Anticipating results from PHYS30202 we have the Hamiltonian

and so in this gauge (ignoring the spin term) ${\hat{H}}^{\left(1\right)}=-eA\cdot p∕m$ and the matrix element is proportional to $⟨f|{\text{e}}^{ik\cdot r}\epsilon \cdot p|i⟩$. Now if $\lambda \gg a_0$, then the phase $k\cdot r$ will scarcely vary as $r$ is integrated over the extent of the atom. The long-wavelength (electric dipole) limit is equivalent to setting ${\text{e}}^{ik\cdot r}=1+ik\cdot r+\dots$ and discarding all terms except the first, as well as ignoring the spin term in the Hamiltonian. The final step then comes in noting that $\widehat{p}=\frac{m}{i\hslash }\left[\hat{r},{\hat{H}}_0\right]$ and $⟨f\left|\left[\hat{r},\hat{H}\right]\right|i⟩=\hslash {\omega }_{fi}⟨f\left|\hat{r}\right|i⟩$. Putting everything together we recover $eℰ⟨f|\epsilon \cdot r|i⟩$ as assumed previously, provided $\omega ={\omega }_{fi}$. As argued above this is a good approximation, unless the leading term vanishes. In other words if a transition cannot take place because the electric dipole matrix element vanishes, we cannot conclude that it cannot take place at all. It will however be much slower, and if a different transition is allowed by the electric dipole selection rules it will be hard to see the “forbidden” transition. Transitions which take place via the neglected terms are successively called magnetic dipole, electric quadruple, magnetic quadruple, electric octupole.... These transitions are important in nuclear physics, but rarely in atomic physics.

So what conditions must a pair of states satisfy for electric dipole transitions to be allowed? We need the matrix element $⟨n^{\prime }{l}^{\prime }{s}^{\prime };j^{\prime }{m}_j^{\prime }\left|r\right|nls;j{m}_j⟩$ to be non-vanishing; for hydrogen of course $s=s^{\prime }=\frac{1}{2}$. It is useful to write $r\left(=x{e}_1+y{e}_2+z{e}_3\right)$ as

The components of $r$ in this spherical basis are referred to as $r_q$, rather than the cartesian $r_i$.

Since the spherical components of $r$ are just the $l=1$ spherical harmonics, we see that acting on a state with a component of $r$ is like coupling in another $l=1$ system. So the usual rules of addition of angular momentum apply, and we see that the electric dipole operator can only cause transitions between systems whose total angular momentum differs by at most one unit. (This is an example of a general theorem that vector operators transfer one unit of angular momentum—the Wigner-Eckhart theorem: see section A.2.) Similarly, the $z$-component of angular momentum can’t change by more than one unit. Hence we have our the selection rules $\Delta j=0,\pm 1$ and $\Delta m_j=0,\pm 1$

However the electric dipole operator is independent of spin. If we look at matrix elements of the form $⟨j^{\prime }{l}^{\prime }{m}_j^{\prime }\left|r_q\right|jl{m}_j⟩$, we see that it reduces to terms of the form $⟨l^{\prime }{m}_l^{\prime }\left|r_q\right|l{m}_l⟩$ which will vanish unless $l+1\ge l^{\prime }\ge \left|l-1\right|$. However there is an extra consideration. The spherical harmonics have good parity: under reflection in the origin they are either odd (for odd $l$) or even (for even $l$). $r$ is odd. Now the integral of an odd-parity function over all angles is clearly zero, so if $l$ is odd (even), $r\left|\right.l{m}_l⟩$ is even (odd) and so $\left|\right.l^{\prime }{m}_l^{\prime }⟩$ must be even (odd) if the angular integral is not to vanish. Therefore we see that $l=l^{\prime }$, while allowed by the rules of addition of angular momentum (if $l\ne 0$), is not allowed by parity conservation. (The rule for the integral of a product of three spherical harmonics is given in section A.2.)

So finally, for hydrogen, we have the following selection rules:

We saw from the example of the decay of the $2p$ state that the rate was proportional to the energy difference cubed. In general states will decay fastest to the lowest state they are allowed to, so states $np$ will decay mostly to $1s$, $nd$ to $2p$ etc. But what about the $2s$ states?

In this course we are not generally concerned with multi-electron atoms, but at this point we should say something about selection rules more generally. First note that as every electron feels the electric field, the dipole operator is $eℰ\epsilon \cdot R$ where $R={\sum }_i{r}_i$, the sum of the individual position vectors. Second we note that while strictly the only good quantum number of an atom is $J$, associated with the total angular momentum $\hat{J}={\sum }_i\left({\hat{L}}_i+{\hat{S}}_i\right)$, for reasonably light atoms $L$ and $S$, corresponding to $\hat{L}={\sum }_i{\hat{L}}_i$ and $\hat{S}={\sum }_i{\hat{S}}_i$, are also “reasonably good” quantum numbers (in the sense that states so constructed are a good zeroth-order approximation to the states of the full Hamiltonian). We are assuming this when we use spectroscopic notation ${}^{\left(2S+1\right)}{L}_J$ for the atomic states. This is called “$LS$ coupling”. In that case we can again say that since the dipole operator is spin-independent spin won’t change ($\Delta S=0$), and coupling a vector operator again means that $L+1\ge L^{\prime }\ge \left|L-1\right|$. This time $\Delta L=0$ is not excluded though, because $L$ isn’t connected to the parity of the atomic state. So for light atoms we have, along with a parity change,

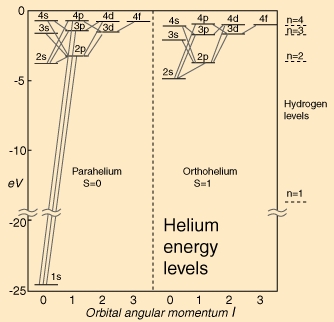
Examples of such allowed transitions are shown in this diagram of the energy levels of helium:

All of these levels have one excited electron and so have the configuration $1snl$. Note that in helium the states of the same $n$ are no longer degenerate as the higher the value of $l$, the more the nuclear charge is screened by the $1s$ electron. Also, triplet states (orthohelium) lie lower than singlet (parahelium), because the latter, having antisymmetric spin wave functions, must have symmetric spatial wavefunctions which bring the electrons closer together and hence increase the Coulomb repulsion. Note that the diagram above doesn’t specify $J$ values.

If $L$ and $S$ are not good quantum numbers, there is still one thing we can say: since $R$ is a vector operator, we must have $J+1\ge J^{\prime }\ge \left|J-1\right|$:

In helium violations of LS coupling will be very small (giving rise to very weak transitions) and will be of similar size to those due to terms ignored in making the dipole approximation. An example is the first excited state of orthohelium, in which one electron is in the $2p$ state and $S=1$, with total $J=1$. According the the electric dipole selection rules in $LS$ coupling it cannot decay to the ground state (which has $S=0$), but the fact that the spin-orbit interaction mixes the $S=0$ and $S=1$ states allows a very weak electric-dipole decay which has only recently been observed.

Violations of the electric dipole selection rules—“forbidden” transitions—must be due to higher-order operators (quadrupole and higher). These allow successively greater changes in $J$. But all orders, $J=0\to J=0$ transitionsare excluded. So for example the ground state of orthohelium (one electron in the $2s$ state and $S=1$) is forbidden from decaying via an electric dipole transition by the parity selection rule. Even magnetic dipole transitions are only allowed through violations of $LS$ coupling , and as a result its lifetime is $10^4$ s. The single-photon decay of the $2s_{1∕2}$ state of hydrogen is a similarly “forbidden” magnetic dipole transition, but in fact the two-photon decay dominates with a lifetime of about 0.1 second.

An example of an absolutely forbidden process is the single-photon decay of the first excited state of parahelium (one electron in the $2s$ state and $S=0$, hence $J=0$). In fact it decays by emitting two photons with a lifetime of $19.7$ ms.

• Gasiorowicz ch 14.3, 17.3
• Mandl ch 6.2– most complete
• Shankar ch 17.2
• (Townsend ch 14.8)

[next] [prev] [up] [top]