Finite width of excited state

4.5 Finite width of excited state

Summary: A full treatment of the eﬀect on states of coupling to radiation is beyond the scope of the course. But we can motivate the fact that a ﬁnite lifetime leads to broadening of the state.

In ﬁrst-order perturbation theory, changes in the initial state are ignored. But in fact we have often been told that a state which can decay with a lifetime $τ$ has an uncertainty in its energy of the order $Δ E = ℏ ∕ τ$ . How does this arise?

At second order in perturbation theory the ﬁrst-order expressions for the coeﬃcients $d_{n}$ ( $n \neq i$ ) give a non-vanishing expression for the rate of change of the initial state $d_{i}$ . The mathematical treatment required to do this properly is too subtle to be worth giving here, but the bottom line is (taking $t = 0$ as the starting time for simplicity)

P_{i \to i} = e^{- Γ_{i} t ∕ ℏ} where Γ_{i} = ℏ \sum_{n} R_{i \to n}

which is exactly as one would expect. $Γ$ , which has units of energy, is called the line width; $ℏ ∕ Γ$ is the total lifetime of the state.

Furthermore if one returns to the derivation of the $d_{n}$ and allows for the fact that $d_{i}$ is decaying exponentially (rather than constant as assumed at that order of perturbation theory) we ﬁnd the integral

\frac{i}{ℏ} \int_{0}^{t} e^{i (ω_{n i} - ω) t^{'} - Γ t^{'} ∕ (2 ℏ)} d t^{'} \to \frac{1}{ℏ (ω_{n i} - ω) + \frac{i}{2} Γ}

The modulus is

\frac{1}{{(E_{n i} - ℏ ω)}^{2} + \frac{1}{4} Γ^{2}}

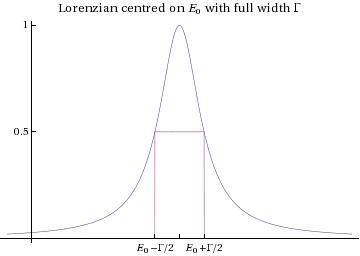
This is a Lorentzian; $Γ$ is the full width at half maximum and its presence tames the energy $δ$ -function we found originally. (Hence sensible results can be found even if there is not a continuum of photon states.) The upshot is that we no longer need exact energy matching for a transition to occur; the energy of an unstable state is not precise, but has an uncertainty: $Δ E \approx Γ = ℏ ∕ τ$ .

Gasiorowicz ch 15.3 (and Supplement 15-A)
Mandl ch 9.5.3

[next] [prev] [up] [top]