PHYS20672 Summary 4

The Residue Theorem

image of mappings

  1. Suppose that we expand a function $f(z)$ about the point $z=a$ in a Laurent series, valid for $0<|z-a| < R$: $$f(z)=\sum_{n=0}^\infty a_n(z-a)^n + \sum_{n=1}^\infty\frac{b_n}{(z-a)^n}\,.$$ Then, for a curve $C$ lying in the region $0<|z-a| < R$, $$\oint_C f(z)\,\d z=2\pi i\, b_1.$$ The coefficient $b_1$ is called the residue of $f(z)$ at $z=a$; in the lectures it is often denoted $\res(a)$.
  2. Hence for a curve $C$ which encloses a number of poles of $f(z)$, the residue theorem states that $$\oint_C f(z)\,\d z=2\pi i \times[\text{sum of residues at all poles inside $C$}].$$
  3. The residue at each pole is the term $b_1$ in the Laurent expansion in the vicinity of that pole; note that this expansion will be different for each pole!
  4. For a function $f(z)$ with a simple pole at $z=a$, we can often use one of the following formulas for the residue: $$b_1=\lim_{z\to a}\bigl[(z-a) f(z)\bigr];\qquad \text{for } f(z)=\frac{g(z)}{(z-a)},\;\; b_1=g(a);\qquad \text{for } f(z)=\frac{g(z)}{h(z)},\;\; b_1=\frac{g(a)}{h'(a)};$$ where $g(z)$ and $h(z)$ represent functions which are analytic at $a$, with $g(a)\ne0$ (and finite) and $h(a)=0$. Note that the first of the above formulas is always applicable and that the others follow easily from it.
  5. For a function $f(z)$ with a pole of order $p$ at $z=a$, then in principle we can find $b_1$ from $$b_1=\frac1{(p-1)!}\lim_{z\to a}\left\{\frac{\d^{p-1} }{\d z^{p-1}}\left[(z-a)^p f(z)\right]\right\}.$$ This formula can be tedious to apply if $p$ is large, but it has a nice self-correcting feature: if you overestimate the order of the pole, the formula still gives the right answer for $b_1$. You should think about why that is.
  6. For higher-order poles, if $f(z)$ can be written as a ratio of analytic functions it can be simpler to use the Taylor expansions for these and hence construct the Laurent series up to $b_1$ explicitly. It is therefore worth knowing the first few terms of the Taylor expansions of familiar functions such as $\e^z$, $\sin z$, $\tan z$, $\ln(1+z)$, etc.

Spiegel 7.1-3

Riley 18.14; Boas 14.5, 14.6 ; Arfken 7.2

Integrals of functions of a real variable, via contour integration

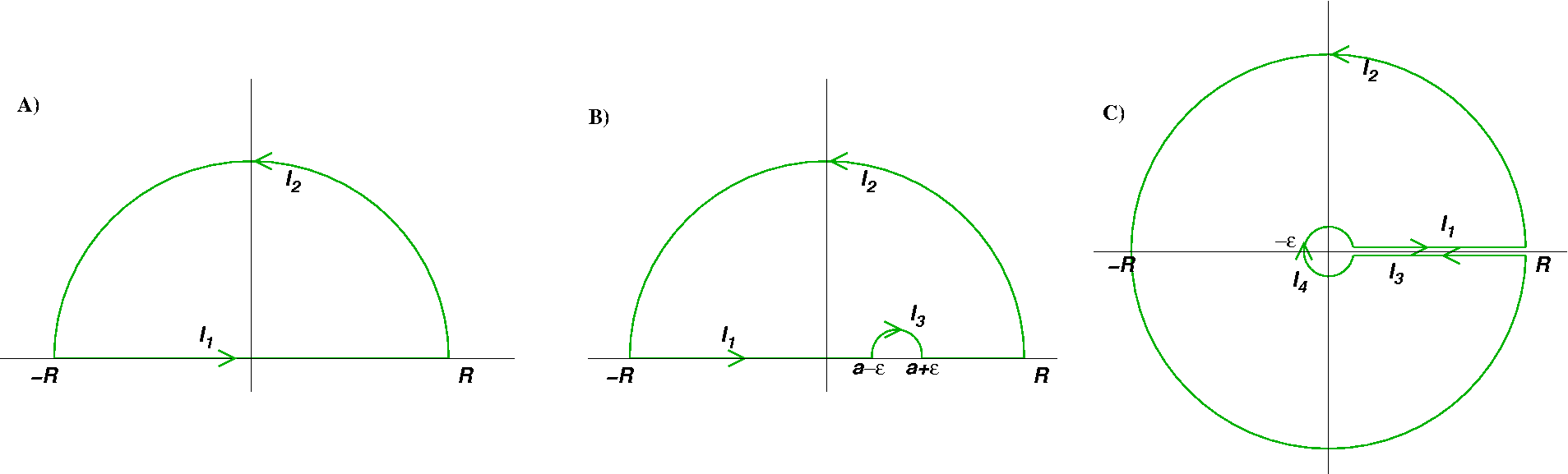
image of mappings

  1. The contours above are examples of contours which can be used to calculate real integrals
  2. If $I=\int_{-\infty}^\infty f(x)\d x$, and $f(z)$ has a finite number of poles none of which are on the real axis, and $|f(R\e^{i\theta})|\to 0$ faster than $1/R$ as $R\to \infty$, then we can use contour $C$ shown in (A). With $R$ large enough so that all poles in the upper half plane are within $C$, $\lim_{R\to\infty}I_2=0$. Hence $$ I=\lim_{R\to\infty}I_1= \lim_{R\to\infty}\left(\oint_C f(z)\,\d z-I_2\right) =2\pi i\times\left[\text{sum of residues at all poles inside $C$}\right]$$
  3. If $I=\int_{-\infty}^\infty f(x)\e^{ikx}\,\d x$, and (i) $k>0$, (ii) $f(z)$ is meromorphic in the upper half plane and (iii) $|f(z)|\to 0$ as $|z|\to \infty$ in the upper half plane, then we can also use contour $C$ shown in (A). The vanishing of $I_2$ as $R\to \infty$ in this case is called Jordan's lemma. If $k<0$, but the other conditions of Jordan's lemma hold for the lower half plane, we can close the contour in the lower half plane instead.
  4. If in either case above there is a pole on the real axis at $z=a$, we define the principal value of the integral to be $$\lim_{\epsilon\to 0}\left[\int_{-\infty}^{a-\epsilon} f(x)\,\d x+\int_{a+\epsilon}^{\infty} f(x)\,\d x\right];\;\text{the limiting value is denoted by}\;\mathrm{P}\!\int_{-\infty}^\infty f(x)\,\d x\quad\text{or}\quad\Pint{-\infty}\infty{f(x)\,\d x}.$$ To evaluate it we use the contour shown in (B). If the pole is simple or of odd order we have $\lim_{\epsilon\to 0}I_3=-i\pi\,b_1$ where $b_1$ is the residue of the pole at $z=a$. If the pole is of even order the principal value of the integral will not exist.
  5. If the integrand has a branch point at $z=0$ we may be able to evaluate $I=\int_{0}^\infty f(x)\,\d x$ through the use of the contour shown in (C), where the branch cut is taken along the positive real axis. The contributions $I_1$ and $I_3$ will not cancel because $f(x)\ne f(x\e^{2\pi i})$.
  6. If $I=\int_{0}^{2\pi} F(\sin\theta,\cos\theta)\,\d \theta$, you may be able to be evaluate the integral through the variable change $z=\e^{i\theta}$, which turns the real $\theta$ integral into a contour integral around the unit circle $\abs z=1$.
  7. Integrands of the form $f(z) \cot z$, $f(z)/ \sin z$, etc., may be used to evaluate series of the form $\sum_i \pm f(x_i)$ where $x_i$ are the zeros of $\tan x$ or $\sin x$. The most convenient contour to use is normally a large square of side $L$, each of whose vertical sides crosses the real axis half way between a pair of poles. Then provided $f(z)$ falls off faster than $1/L$ as $L\to\infty$, the contour integral will tend to zero.

Spiegel 7.4-8

Riley 18.16-19; Boas 14.7; Arfken 7.2