Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.4 Moment-of-inertia tensor |
Previous: 4.2 Rigid bodies |
A tensor,
like a vector, is a mathematical object with a geometrical meaning.
A tensor acts on a vector to produce a new vector which is linearly related to
the old one but points in a different direction (in general). In some
coordinate basis, the components of a tensor form a ![]() matrix. However
the action of a tensor on a vector is independent of the basis we use to
represent them and so its geometrical meaning is invariant.
matrix. However
the action of a tensor on a vector is independent of the basis we use to
represent them and so its geometrical meaning is invariant.
An important physical example is the stress tensor
![]() which relates the force transmitted across some
surface in a solid to the (vector) area
which relates the force transmitted across some
surface in a solid to the (vector) area
![]() of that surface:
of that surface:
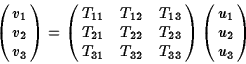
This is a linear operation and so it satisfies the distributive laws
The unit tensor
![]() leaves all vectors
unchanged:
leaves all vectors
unchanged:
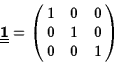
You should be familiar with the scalar and vector product of two vectors.
There is a third way to multiply two vectors: the dyadic product which
yields a tensor. It is denoted
![]() and has components
and has components
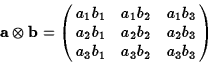
This type of tensor is also known as a second-rank tensor, where the rank refers to the number of indices on its components. A scalar can be thought of as a zeroth-rank tensor and a vector as a first-rank tensor. More complicated kinds also exist. The crucial property of a tensor is that that its components should transform under a rotation of coordinate axes in such a way as to keep its geometrical or physical meaning invariant.
More on tensors: This type of tensor is also known as a second-rank tensor, where the rank refers to the number of indices on its components. A scalar can be thought of as a zeroth-rank tensor and a vector as a first-rank tensor. More complicated kinds also exist. The crucial property of a tensor is that that its components should transform under a rotation of coordinate axes in such a way as to keep its geometrical or physical meaning invariant.
Textbook references
Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.4 Moment-of-inertia tensor |
Previous: 4.2 Rigid bodies |
Mike Birse
21st July 2000