Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.9 Gyroscopes |
Previous: 4.7 The symmetric top |
Let us now look at free rotations of a general body, with three different
principal moments of inertia,
If q body rotates about a principal axis, then it is dynamically balanced: no torque is required to maintain the rotation. Such motion is stable if small perturbations of the axis of rotation just lead to oscillations around the balanced configuration.
To determine whether this is the case, consider a body rotating about an
axis very close to one of its principal axes, say the axis ![]() with the
smallest principal moment. The angular velocity can be written
with the
smallest principal moment. The angular velocity can be written
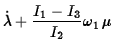 |
|||
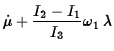 |
These equations can be decoupled to give an equation for ![]() ,
,
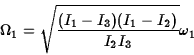
The symmetry of Euler's equations under cyclic permutations of the indices
means that we can us this to write down the results for small perturbations
of rotations about the other two principal axes. In the case of rotations close
to ![]() ,
the axis with the largest principal moment, the motion is
similar to that for
,
the axis with the largest principal moment, the motion is
similar to that for ![]() .
.
However, rotations close to ![]() ,
the axis with the intermediate
principal moment, show a quite different behaviour. In this case the
``frequency'' for small perturbations is imaginary. This shows that the
solutions are not oscillatory but instead exponential:
,
the axis with the intermediate
principal moment, show a quite different behaviour. In this case the
``frequency'' for small perturbations is imaginary. This shows that the
solutions are not oscillatory but instead exponential:
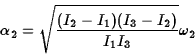
This analysis shows that rotations about the principal axes with the largest or smallest moments are stable. In contrast rotations about the principal axis with the intermediate moment are unstable.
Finally, for a body with an axis of symmetry, rotations the symmetry axis are stable, as we saw before. For rotations about the other two principal axes, the frequency of small perturbations is zero. This implies that these rotations are marginally (un)stable: small perturbations do grow with time, but only linearly.
Textbook references
Home: PC 1672 home page |
Up: 4 Rigid-body motion |
Weekly plan |
Help: Guide to using this document |
Next: 4.9 Gyroscopes |
Previous: 4.7 The symmetric top |
Mike Birse
17th May 2000