Home: PC 1672 home page |
Up: 2 Noninertial frames . . . |
Weekly plan |
Help: Guide to using this document |
Next: 3 Gravitation |
Previous: 2.4 The weather |
PC1672 Advanced dynamics
2.5 Foucault's pendulum
The small effects of the Coriolis force can also become appreciable if motion
persists for a long time. The classic demonstration of this is the
pendulum devised by Foucault. This is a very long pendulum, free
to swing in any horizontal direction.
In the rotating reference frame of the Earth, the pendulum bob moves under
the influence of the horizontal component of the tension in the string and
the Coriolis force. The equations describing its motion are
The second term in each equation is the Coriolis effect, proportional to the
vertical component of the Earth's angular velocity
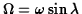 .
The last term is the usual restoring force on the bob, with
.
The last term is the usual restoring force on the bob, with
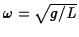 being the natural frequency of the pendulum.
being the natural frequency of the pendulum.
The equations are two coupled linear ODE's. To solve them, we take a trial
solution of the form
Substituting this into the equations of motion leads to two linear equations
which can be written in matrix form as
This is a generalised eigenvalue problem: nontrivial solutions exist only if
the determinant of the matrix vanishes. This leads to an auxiliary equation
which has four solutions for 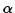 .
(Since we started with two second-order
ODE's, we expect to have four independent complementary functions.)
.
(Since we started with two second-order
ODE's, we expect to have four independent complementary functions.)
A neater approach (used in M) is to combine the two real equations into
a single complex one by defining the complex coordinate
The equations of motion can then be written
In this form the Coriolis term looks like a damping term, except for the fact
that its coefficient is imaginary. Using a trial solution of the form
leads to the auxiliary equation
This has two roots
Whatever approach we use to solve the equations, we find that they have
solutions of the form
These describe oscillations of the pendulum with a frequency that is very
close to the natural one 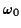 .
The plane of the oscillations
precesses at a rate
.
The plane of the oscillations
precesses at a rate 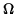 .
In the northern hemisphere, this precession is clockwise as seen from above,
reflecting the rightwards deflection of the motion by the Coriolis force.
The rate of precession is equal to the vertical component of the Earth's
angular velocity. (From an inertial observer's point
of view, the pendulum is just trying to keep swinging in the same plane, while
the Earth turns underneath it.)
.
In the northern hemisphere, this precession is clockwise as seen from above,
reflecting the rightwards deflection of the motion by the Coriolis force.
The rate of precession is equal to the vertical component of the Earth's
angular velocity. (From an inertial observer's point
of view, the pendulum is just trying to keep swinging in the same plane, while
the Earth turns underneath it.)
Here in Manchester, at latitude
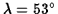 ,
the rate of precession is
,
the rate of precession is
Textbook references
- K&K 8.5, example 8.11
- F&C 5.5
- B&O 7.4
- M 11.4, example 11.4(c)
- M&T 10.4
Home: PC 1672 home page |
Up: 2 Noninertial frames . . . |
Weekly plan |
Help: Guide to using this document |
Next: 3 Gravitation |
Previous: 2.4 The weather |
Mike Birse
17th May 2000
![]() ,
the rate of precession is
,
the rate of precession is