4.5 Adiabatic demagnetisation and the third law of thermodynamics

Take-home message: The properties of a paramagnet can be put to practical use to achieve low temperatures, but we can never get to absolute zero.

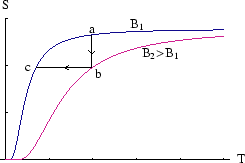
By magnetising and demagnetising a paramagnetic sample while controlling the heat flow, we can lower its temperature.

We start with the sample in a magnetic field $B_1$ at an (already fairly low) temperature $T_1$.

a$\to$ b: With the sample in contact with a heat bath at $T_1$, we increase the magnetic field to $B_2$.
b$\to$ c: With the sample now isolated, we slowly decrease the field to $B_1$ again. This is the adiabatic demagnetisation step; because the process is slow and adiabatic, the entropy is unchanged.

By following these steps on a $T-S$ plot, we see that the second, constant entropy, step, reduces the temperature. The entropy is a function of $B/T$ only, not $B$ or $T$ separately (see here) so if we reduce $B$ at constant $S$, we reduce $T$ also.

The following figure shows what is happening to the spins.

In the first step we increase the level spacing while keeping the temperature constant, so the population of the upper level falls. In the second step we reduce the level spacing again, but as the spins are isolated there is no change in level occupation. The new, lower level occupation is now characteristic of a lower temperature than the original one.

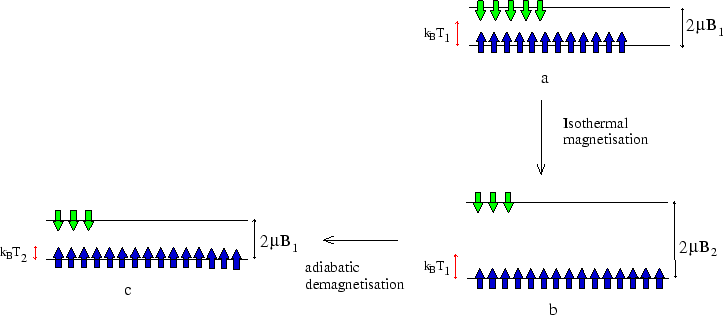
If we start with a large sample, we could repeat the process with a small sub-sample, the remaining material acting as a heat bath during the next magnetisation. By this method temperatures of a fraction of a Kelvin can be reached. However after a few steps less and less is gained each time, as the curves come together as $T\to 0$. (Once the electron spins are all ordered, one can start to order the nuclear spins, and reach even lower temperatures--the magnetic moment of the nucleus is around a two-thousandth of that of the atom), but even that has its limits. (Wondering why we can't just take $B_1$ to zero? See here for the real paramagnet.)

This is an important and general result. There is always a minimum excitation energy $\varepsilon$ of the system, and once $k_{\scriptscriptstyle B}T\ll \varepsilon$ there is no further way of lowering the temperature. The unattainability of absolute zero is the third law of thermodynamics.

References

• Mandl 5.6